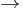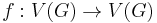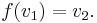Vertex-transitive graph

Graph families defined by their automorphisms
distance-transitive	$\rightarrow$	distance-regular	$\leftarrow$	strongly regular
$\downarrow$
symmetric (arc-transitive)	$\leftarrow$	t-transitive, t ≥ 2
$\downarrow$ _{(if connected)}
vertex- and edge-transitive	$\rightarrow$	edge-transitive and regular	$\rightarrow$	edge-transitive
$\downarrow$		$\downarrow$
vertex-transitive	$\rightarrow$	regular
$\uparrow$
Cayley graph		skew-symmetric		asymmetric

In the mathematical field of graph theory, a vertex-transitive graph is a graph G such that, given any two vertices v₁ and v₂ of G, there is some automorphism

$f:V(G) \rightarrow V(G)\$

such that

$f(v_1) = v_2.\$

In other words, a graph is vertex-transitive if its automorphism group acts transitively upon its vertices.^[1] A graph is vertex-transitive if and only if its graph complement is, since the group actions are identical.

Every symmetric graph without isolated vertices is vertex-transitive, and every vertex-transitive graph is regular. However, not all vertex-transitive graphs are symmetric (for example, the edges of the truncated tetrahedron), and not all regular graphs are vertex-transitive (for example, the Frucht graph).

1 Finite examples
2 Properties
3 Infinite examples
4 See also
5 References

Finite examples

Finite vertex-transitive graphs include the symmetric graphs (such as the Petersen graph, the Heawood graph and the vertices and edges of the Platonic solids). The finite Cayley graphs (such as cube-connected cycles) are also vertex-transitive, as are the vertices and edges of the Archimedean solids (though only two of these are symmetric).

Properties

The edge-connectivity of a vertex-transitive graph is equal to the degree d, while the vertex-connectivity will be at least 2(d+1)/3.^[2] If the degree is 4 or less, or the graph is also edge-transitive, or the graph is a minimal Cayley graph, then the vertex-connectivity will also be equal to d.^[3]

Infinite examples

Infinite vertex-transitive graphs include:

infinite paths (infinite in both directions)
infinite regular trees, e.g. the Cayley graph of the free group
graphs of uniform tessellations (see a complete list of planar tessellations), including all tilings by regular polygons
infinite Cayley graphs
the Rado graph

Two countable vertex-transitive graphs are called quasi-isometric if the ratio of their distance functions is bounded from below and from above. A well known conjecture states that every infinite vertex-transitive graph is quasi-isometric to a Cayley graph. A counterexample has been proposed by Diestel and Leader.^[4] Most recently, Eskin, Fisher, and Whyte confirmed the counterexample.^[5]

References

^ Godsil, Chris; Royle, Gordon (2001), Algebraic Graph Theory, Graduate Texts in Mathematics, 207, New York: Springer-Verlag .
^ Godsil, C. and Royle, G. (2001), Algebraic Graph Theory, Springer Verlag
^ Babai, L. (1996), Technical Report TR-94-10, University of Chicago [1]
^ Diestel, Reinhard; Leader, Imre (2001), "A conjecture concerning a limit of non-Cayley graphs", Journal of Algebraic Combinatorics 14 (1): 17–25, doi:10.1023/A:1011257718029, http://www.math.uni-hamburg.de/home/diestel/papers/Cayley.pdf .
^ Eskin, Alex; Fisher, David; Whyte, Kevin (2005). "Quasi-isometries and rigidity of solvable groups". arXiv:math.GR/0511647. .

Vertex-transitive graph

Contents

Finite examples

Properties

Infinite examples

See also

References